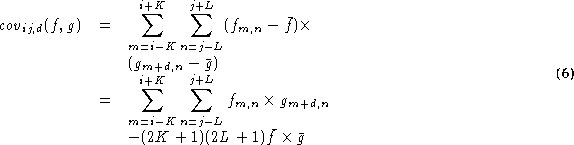
Here again we will use the technique described in Section 2.1 to achieve fast calculation of the cross correlation. Rewriting Equation (2), we have:
Equation (6) is the numerator of Equation (1). Most, if not all, of the image correlation in the literature is performed using direct calculation of Eq. (6). Direct calculation of equation (6) has (2K+1)(2L+1) redundancies. Similar to the calculation for the variance, cross correlation of two images can be obtained using only a few multiplications.
In our case, the correlation is performed along the epipolar line. If for any point in the left image, the search window is assumed to be within [-w, +w] in the right image, then the value of d in equation (6) varies from -w to +w. The traditional way of obtaining the correlation is to fix a point in the left image and vary d in the range of [-w, +w] to calculate the correlation coefficients.
In our new algorithm for fast correlation, we first fix on one particular d all the points in the left image and calculate the cross correlation between the left image and the shifted right image of the amount d. Then we increase the number of d by 1, and repeat the process of correlation calculation until the value of d has gone through [-w, +w].
The complexity of the algorithm is O(MND), where M, N are the image row and column numbers and D is the maximum disparity search range.